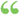 That whenever the summit of the mountains which extend in a direction parallel to the coast from the 56th degree of north latitude to the point of intersection of the 141st degree of west longitude shall prove to be at the distance of more than ten marine... That whenever the summit of the mountains which extend in a direction parallel to the coast from the 56th degree of north latitude to the point of intersection of the 141st degree of west longitude shall prove to be at the distance of more than ten marine...  The Century Illustrated Monthly Magazine - 203 psl.redagavo - 1892Visos knygos peržiūra The Century Illustrated Monthly Magazine - 203 psl.redagavo - 1892Visos knygos peržiūra - Apie šią knygą
 | E. Jerome Dyer - 1898 - 304 psl.
...latitude to the point of intersection of 141 deg. W. longitude, shall prove to be at a distance of more than ten marine leagues from the ocean, the limit...possessions and the line of coast which is to belong to Eussia shall be formed by a line parallel to the windings of the coast, and which shall never exceed... | |
 | United States. Department of the Treasury. Special Agents Division - 1898 - 1118 psl.
...degree of west longitude shall prove to be at the distance of more than ten marine leagues from tbe ocean, the limit between the British possessions and...coast which is to belong to Russia, as above mentioned (that is to say, the limit to the possessions ceded by this convention), shall be formed by a line... | |
 | 1898 - 944 psl.
...the point of Intersection of Hi degrees of west longitude, shall prove to be a distance of more th«n ten marine leagues from the ocean the limit between the British possessions and the line of const which Is to belong to Russia, as above mentioned shall be formed by n line parallel to the widening... | |
 | Robert Stein - 1898 - 404 psl.
...between latitude 56° and the intersection of the 141st meridian shall prove to be at a distance of more than ten marine leagues from the ocean, the limit between the British possessions and the strip of coast now belonging to the United States shall be formed by a line following the windings... | |
 | 1898 - 436 psl.
...marine leagues (30 geographical miles, or about 34£ statutory miles) from the ocean, the boundary shall be formed by a line parallel to the windings of the coast, and never more than ten marine leagues therefrom. To fully understand these provisions topographical information... | |
 | Frederick Schwatka - 1898 - 466 psl.
...the point of intersection of the 141st degree of west longitude shall prove to be at the distance of more than ten marine leagues from the ocean, the limit between the British possesssion and the line of coast which is to belong to Russia as above mentioned (that is to say,... | |
 | Albert Shaw - 1899 - 1046 psl.
...intersection of the one hundred and forty-first degree of west longitude, shall prove to be at a distance of more than ten marine leagues from the ocean, the limit...shall be formed by a line parallel to the windings (sinuosities) of the coast, and which shall never exceed the distance of ten marine leagues therefrom.... | |
 | Albert Shaw - 1899 - 890 psl.
...of the one hundred and forty- first degree of west longtitude, shall prove to be at the distance of more than ten marine leagues from the ocean, the limit...is to belong to Russia as above mentioned shall be found by a line parallel to the windings of the coast, and which shall never exceed the distance of... | |
 | 1899 - 788 psl.
...intersection of the one hundred and forty-first degree of west longitude, shall prove to be at a distance of more than ten marine leagues from the ocean, the limit...which is to belong to Russia as above mentioned shall 1м- formed by a line parallel to the windings (sinuosities) of the coast, and which shall never exceed... | |
 | United States. Congress. Senate. Foreign Relations - 1899 - 820 psl.
...the point of intersection of the 141st degree of west longitude shall prove to be at the distance of more than ten marine leagues from the ocean, the limit...coast which is to belong to Russia as above mentioned (that is to say, the limit to the possessions ceded by this convention) shall be formed by a line parallel... | |
| |